As a quick recap, in part 1 we explained integration: finding the area underneath a line; then, we used integration to find the total amount of lemonade sold up to each day.
But, what is the other fundamental process? Suppose a manager sees the graph of total amount of lemonades sold up to a certain day (y=2x), and the manager wants to know how much lemonade you sold on each day; this is a simple problem as well: you only have to subtract the total lemonade you sold up to the previous day from the total lemonade you sold up to today. However, this is actually exactly the same as finding the slope of a line! This is the other fundamental process of calculus called derivation: finding the slope of a line at a given point.
If we find the slope of our line y=2x at each day, we would always get the value of 2, and if we record this slope value across all days, we would actually return to our previous graph of y=2; this process of derivation obtains the manager’s goal of finding how much lemonade you sold each day.
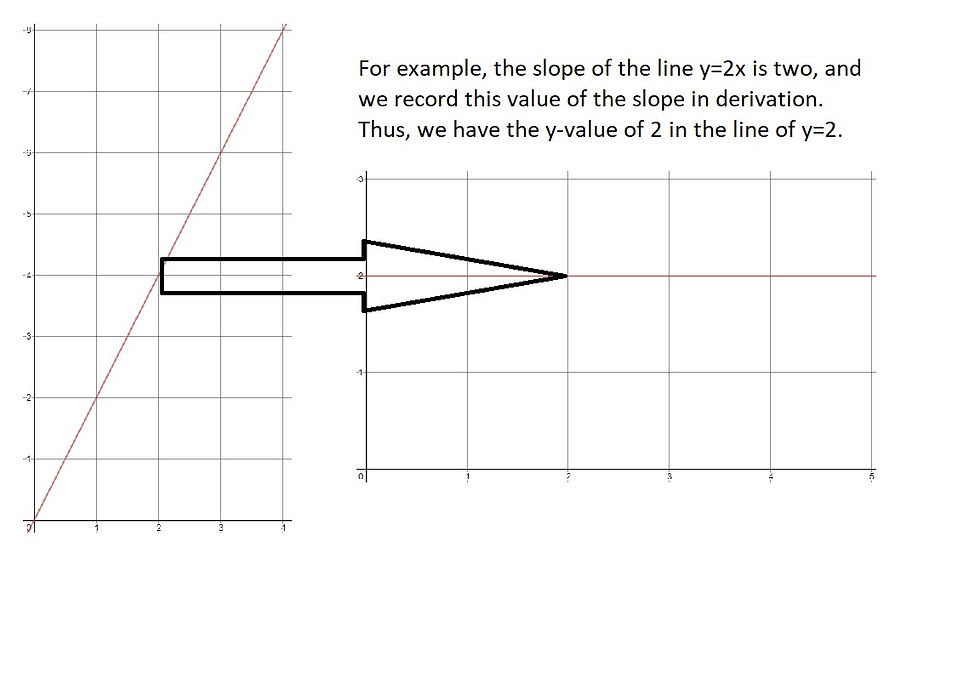
So, if integration is finding the total lemonade sold up to each day from lemonade sold each day, and derivation is finding lemonade sold each day from total lemonade sold up to each day, we can see that integration and derivation are in fact opposite of each other.
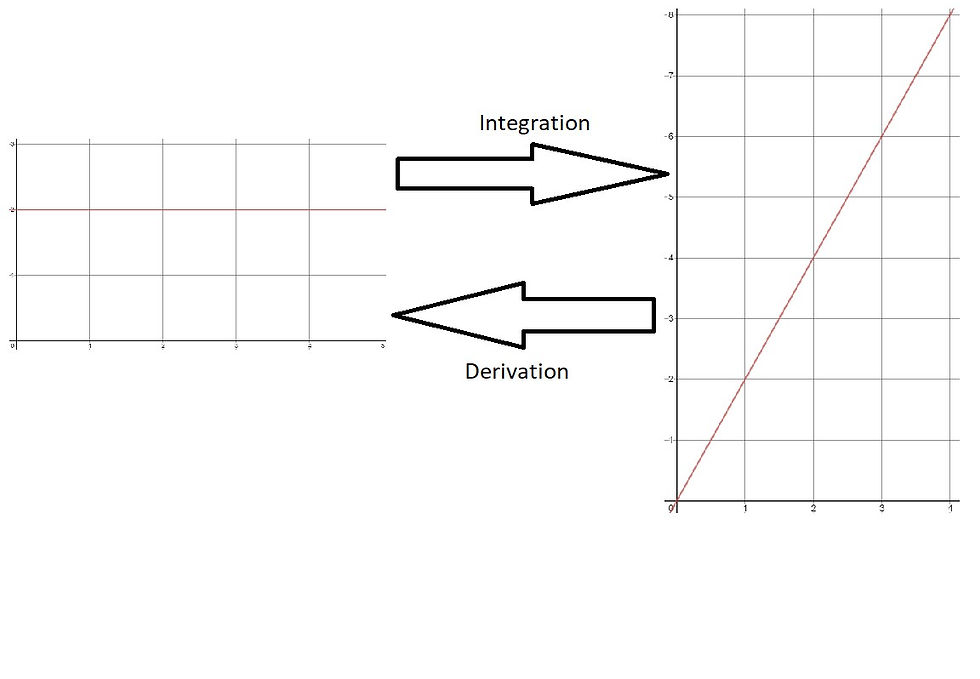
To summarize what we learned: integration is finding the area between a function and the x-axis and recording the value of the area as the y-value of a new function; derivation is finding the slope of a function and record the value of the slope as the y-value of a new function.
Integration and derivation are the essence of calculus, and the actual difficulty of calculus comes from more complicated functions, more variables, and combinations of integration and derivation. Don’t be discouraged however, because if you understood this article, you have understood the purpose of calculus, and in the future, calculus will be 100 times easier for you.
Comments